Sådan bliver du god til at løse Futoshiki-opgaver

I den følgende vejledning gennemgår vi trin for trin grundlæggende og avancerede teknikker til at løse Futoshiki-opgaver, med illustrationer, der viser metoderne på konkrete eksempler.

Udgangspunktet for at finde en løsning er selve spillets definition: I Futoshiki skal du udfylde brættet, så hvert ciffer forekommer én gang i hver række og kolonne, og så brættets uligheder overholdes. Ud fra dette kriterium kan du komme tættere på løsningen ved trin for trin at udfylde tomme felter med de cifre, der er den eneste måde at overholde brættets begrænsninger på.

Udelukkelse via kolonner og rækker

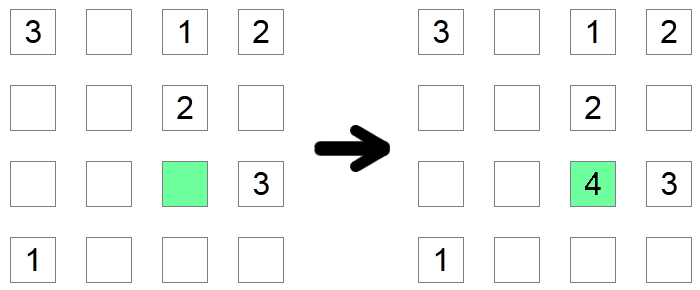
Hvis et felts kolonne og række tilsammen allerede indeholder alle mulige cifre undtagen ét, skal feltet indeholde det manglende ciffer. I eksemplet ovenfor skal det grønne felt være 4, fordi det ikke kan have nogen anden værdi: de andre mulige cifre findes allerede i dets række eller kolonne.

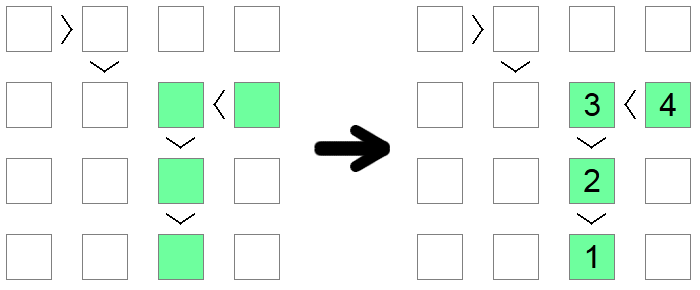
Kæde af uligheder

Hvis du ser en kæde af uligheder, enten < (alle stigende) eller > (alle faldende), der er lige så lang som brættets størrelse, skal kæden være rækkefølgen fra 1 op til brættets størrelse. Kædens længde garanterer, at denne rækkefølge er den eneste mulige løsning, der opfylder den monotone betingelse, som ulighedskæden stiller.

Tvungne minimums- og maksimumsværdier

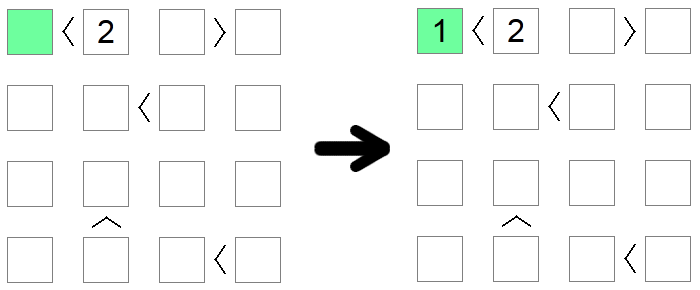
Felter, der er mindre end 2, må nødvendigvis have værdien 1, da det er den eneste tilladte værdi på brættet, der opfylder den betingelse. Tilsvarende skal felter, der er større end brættets størrelse minus 1, være lig med brættets størrelse. I eksemplet ovenfor er den eneste mulige værdi for det grønne felt (mindre end 2) 1.

Udelukkelse af minimums- og maksimumsværdier

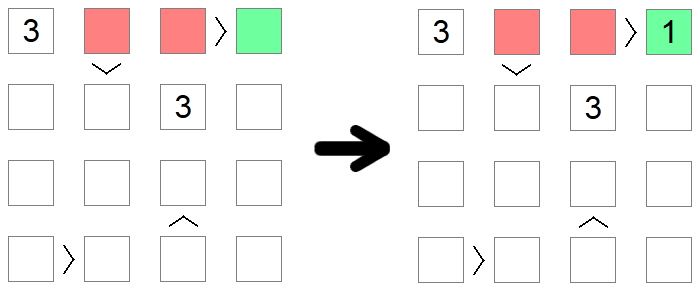
Felter, der er større end andre felter, kan ikke være 1, den laveste tilladte værdi på brættet, da der ikke findes nogen værdi mindre end 1. Tilsvarende kan felter, der er mindre end andre felter, ikke indeholde den højeste tilladte værdi, da der så ikke ville være noget større at sætte på den anden side af uligheden. I eksemplet ovenfor kan 1 ikke stå i de røde felter, da de alle er større end andre felter på brættet, så det eneste mulige sted til 1 i brættets første række er det grønne felt.

Kombination af regler

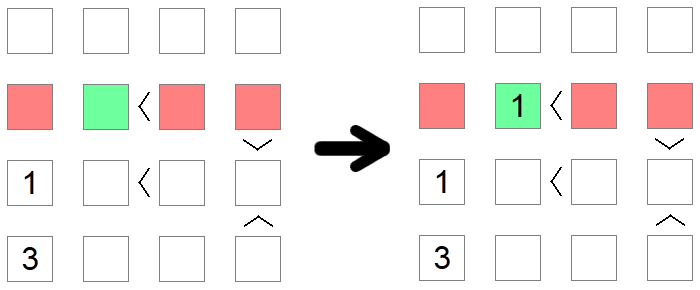
Nogle gange skal flere regler bruges sammen for at nå frem til en konklusion. Det er tilfældet i eksemplet ovenfor, hvor vi prøver at placere værdien 1 i brættets anden række. Det første røde felt udelukkes på grund af kolonneudelukkelse (vi har allerede et 1-tal i den kolonne), mens det andet og tredje røde felt udelukkes på grund af udelukkelse af minimumsværdier, da der er 'større end'-uligheder knyttet til dem. Derfor er det grønne felt det eneste mulige sted at placere 1 i den række.

Gennemprøvning af muligheder

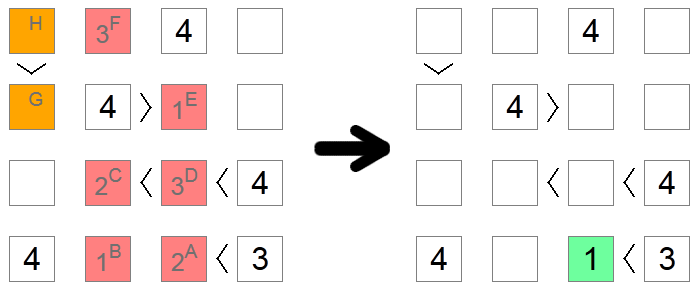
Nogle gange, især på svære brætter, er der ingen anden måde at finde det rigtige ciffer til et felt på end at undersøge konsekvenserne af hver mulighed, indtil man når en modstrid. I eksemplet ovenfor er alle røde og orange felter tomme fra starten. Vi vil finde ud af, om felt A indeholder 1 eller 2. Vi antager, at det indeholder 2, og undersøger, om den antagelse fører til en modstrid.

Hvis felt A er 2, må felt B være 1 (den eneste tilbageværende værdi i nederste række). Felt C kan være 1 eller 2, da det indgår i en kæde af uligheder, som kræver 2 større tal, men nu kan det ikke være 1 på grund af kolonneudelukkelsen fra felt B, så felt C er 2, og felt D er 3 (den eneste værdi mellem 2 og 4). På grund af kolonneudelukkelser er felt E 1, og felt F er 3.

Ser vi nu på de orange felter, opdager vi modstriden: Hvis felt G var 2, skulle felt H være enten 3 eller 4, hvilket ikke er tilladt på grund af rækkeudelukkelse. Hvis felt G var 3, skulle felt H være 4, hvilket ikke er tilladt af samme grund. Da der ikke er flere mulige værdier tilbage til felt G, er vi kørt fast, og vores oprindelige antagelse var forkert: 2 er ikke et gyldigt træk i felt A, så vi kan roligt placere 1 der, den eneste anden mulige værdi.

Konklusioner

Ovenfor har vi vist, hvordan man løser en Futoshiki-opgave med en række teknikker, der kan hjælpe dig med at udlede det næste træk, selv i svære situationer. Den anden vigtige ingrediens, hvis du vil blive dygtig og hurtig til at løse Futoshiki-opgaver, er erfaring: jo mere du øver dig, jo bedre og hurtigere bliver du.

Hvis du er klar til en udfordring, kan du spille en tilfældig Futoshiki-opgave lige nu ved at klikke på knappen nedenfor. Held og lykke!

Spil Futoshiki